Algèbre linéaire

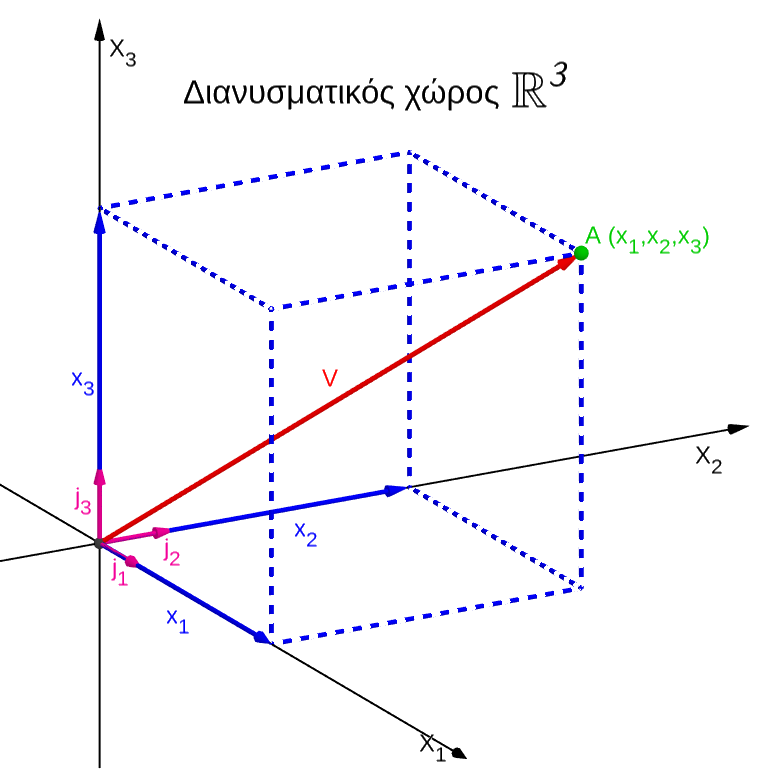
Notions de base d'algèbre linéaire (sous-espace vectoriel, de base, applications linéaires, ...)

Analyse complexe

  • Nombres et fonctions complexes
  • Fonctions holomorphes
  • Théorème de Cauchy
  • Formule de Cauchy
  • Séries de Taylor et de Laurent
  • Théorème des résidus et applications
  • Principes d'analyse complexe

Compléments de mathématiques

Diverses notions de convergence de suites de fonctions (simple, uniforme,...)
Série et transformée de Fourier
Espace de Hilbert
Introduction à la théorie des distributions

Introduction aux variétés différentielles

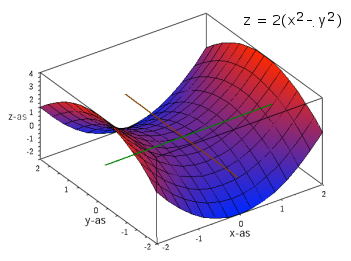
Courbes paramétrées : définitions, propriétés locales, propriétés métriques des courbes paramétrées (reparamétrisation par longueur d'arc, courbure, torsion, trièdre de Frenet).

Surfaces paramétrées de R3 : définitions, propriétés locales (plan tangent, vecteur normal,...), propriétés métriques des surfaces paramétrées (première et seconde formes fondamentale, courbure normale, courbures principales, courbure de Gauss).

Mathématiques effectives

Jeux sous forme stratégique, stratégie dominée/dominante, jeux à somme nulle, notion de valeur, point de selle, théorème du MinMax, jeux à somme non-nulle, équilibre de Nash en stratégies pures et mixtes, théorème de Nash, jeux bayesien, équilibre bayesien, jeux sous forme extensive, équilibre parfait en sous-jeux, jeux répétés, "Folk Theorem".

Mathématiques discrètes

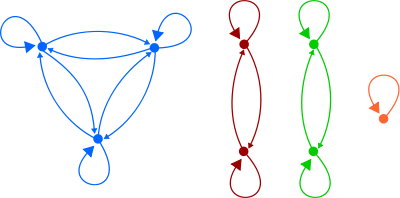
  • Notions d'arithmétique (étude des nombres entiers)
  • Les relations binaires (incluant relations d'ordre et d'équivalence)

Méthodes formelles pour la conception de systèmes

  • Introduction aux méthodes formelles.
  • Modélisation de systèmes. Linear temporal logic. Computation tree logic. Model checking symbolique. Vérification de systèmes probabilistes (et quantitatifs). Synthèse de systèmes probabilistes (et quantitatifs). Synthèse via la théorie des jeux. Présentations d'outils logiciels par les étudiants.
  • Lecture et présentation de travaux avancés en vérification et synthèse de systèmes informatiques. Projet : conception d'un système à l'aide de méthodes formelles.