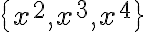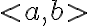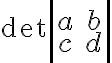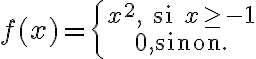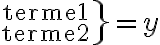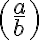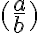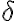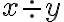délimiteurs (résumé)
| Délimiteurs (parenthèses, accolades, crochets, ...)
|
| Commande
|
Exemple
|
Résultat
|
|
\left( ... \right) ou (...)
|
$$2 ( a+b )$$
|
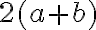
|
| \left[ ... \right] ou [...]
|
$$[a^2+b^2]$$
|
![[a^2+b^2] [a^2+b^2]](https://moodle.umons.ac.be/filter/tex/pix.php/794a308339fcb27204376484c2d233f9.png)
|
| \left\{ ... \right\} ou \{...\}
|
$$\{x^2, x^3, x^4\}$$
|
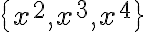
|
| \left< ... \right> ou < ... >
|
$$< a,b >$$
|
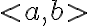
|
| \left| ... \right| ou | ... |
|
$$\det\left|\begin{matrix}a&b\\ c&d \end{matrix}\right|$$
|
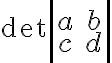
|
|
\left\{ ... \right. ou \{ ...
(remarquer le point !)
|
$$f(x)=\left\{{x^2, \text{ si } x\geq -1\atop 0, \text{sinon.}}\right.$$
(\text permet d'insérer du texte en romain)
|
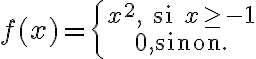
|
|
\left. ... \right\} ou ... \}
(remarquer le point !)
|
$$\left.{\text{terme1}\atop\text{terme2}}\right\} = y$$
|
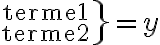
|
|
|
|
|
Remarque : La dimension des délimiteurs s'adapte automatiquement par l'utilisation de \left et \right. Par exemple, lorsque le commutateur \displaystyle est utilisé pour modifier la taille des formules :
$$\displaystyle \left( \frac{a}{b} \right)$$ donne 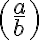
$$\displaystyle ( \frac{a}{b} )$$ donne 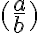 | 


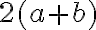
![[a^2+b^2] [a^2+b^2]](https://moodle.umons.ac.be/filter/tex/pix.php/794a308339fcb27204376484c2d233f9.png)