Optimal Estimation

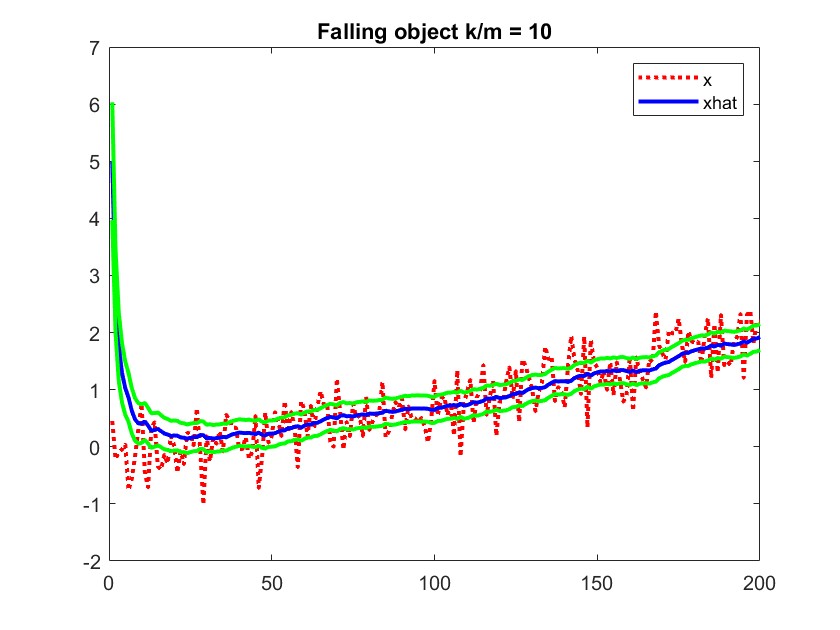
Représentation stochastique des systèmes dynamiques; filtrage de Kalman et extensions; observateur à horizon glissant; exercices.

Optimal Control

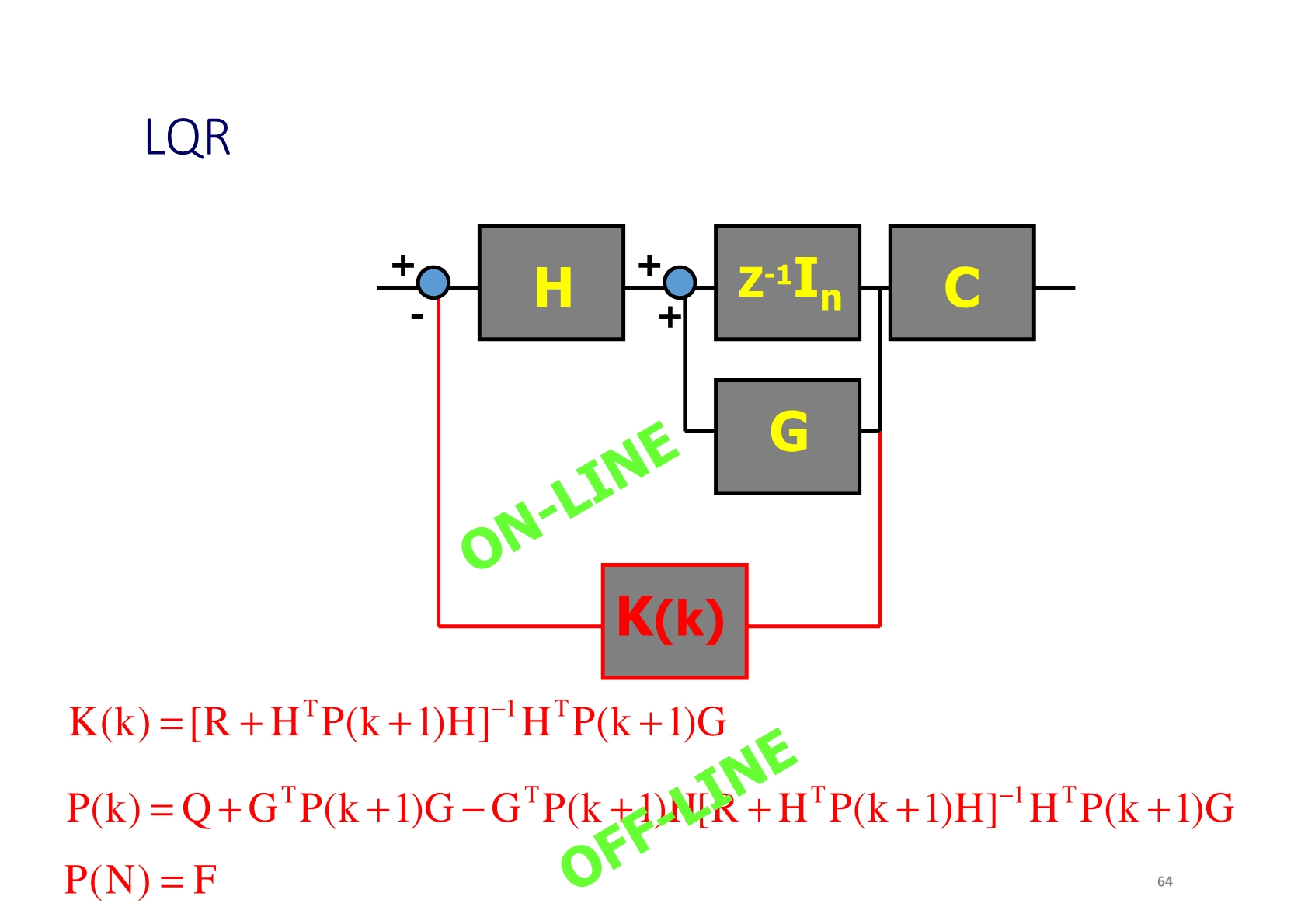
Régulateur linéaire quadratique; principe du maximum de Pontryagin; optimisation dynamique et commande prédictive; exercices.

Control of Energy Systems

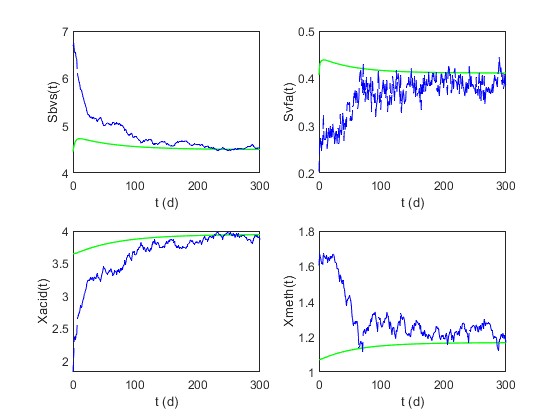
Exploitation de concepts vus dans le cours "Control of Multivariable Systems" et introduction de concepts nouveaux en modélisation, estimation et commande des systèmes illustrées par des applications particulières (études de cas).

Control of Multivariable Systems

   

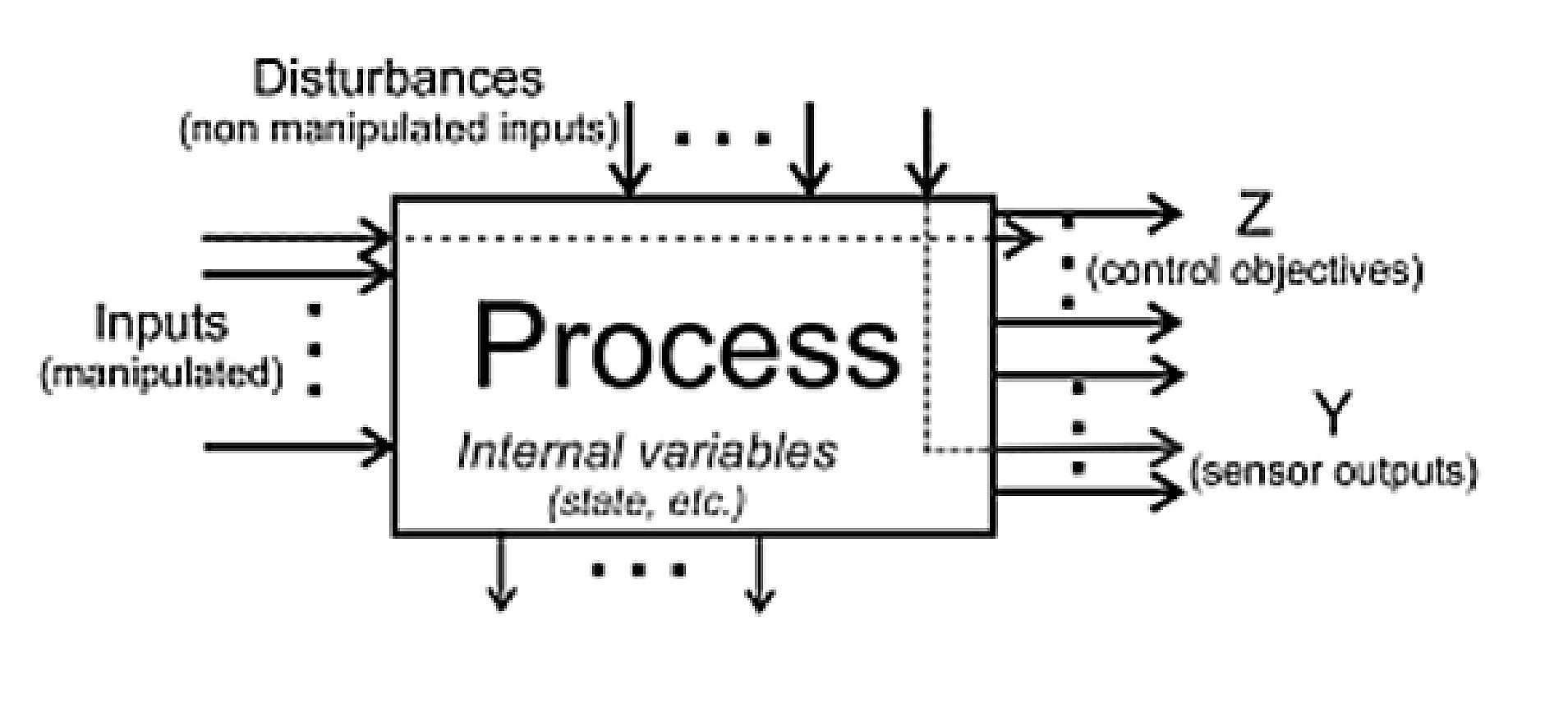
This course introduces various topics related to dynamic multivariable systems:

  • (continuous-time and discrete-time) state equations;
  • stability analysis;
  • controllability and observability;
  • subspace identification;
  • state feedback control;
  • state estimation and observer design for deterministic continuous-time and discrete-time systems.

Commande des procédés

Mons

Commande à temps continu : autres contrôleurs que le PID; synthèse des contrôleurs vis à vis de la perturbation; conception d'un système anti windup; lieux d'Evans; boucles de type cascade; commande par modèle; prédicteur de Smith;

Commande numérique : transformée en z; transmittance en z équivalente du procédé à temps continu; stabilité, précision et calcul de contrôleur d'une boucle numérique.

Commande des procédés

Charleroi

  • Modélisation et analyse des systèmes : approche de modélisation ; linéarisation ; étude des systèmes du premier, du second ordre et d'ordre quelconque, conditions de stabilité; notions de modèle d'état ;
  • Fonctionnement en boucle fermée : principe ; analyse de la stabilité en boucle fermée, concepts de précision et de performances transitoires ;
  • Dimensionnement de régulateurs PID : stabilisation et contrôle par contrôleurs PID; méthodes expérimentales de réglage des contrôleurs PID.

Motion Control

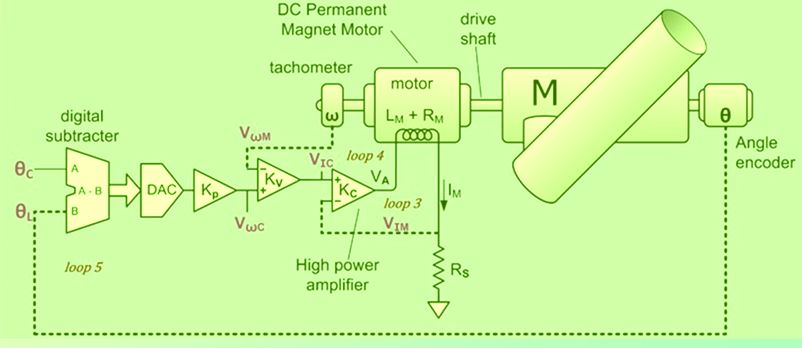
This course is devoted to electric actuators and discusses their characteristics and selection criteria depending on the application. The focus is on DC motors and stepper motors. Mathematical modeling of actuators and regulator design is discussed, including classic regulators (on-off and PID), RST control, and optimal and predictive control.

Nonlinear Modeling of Biosystems

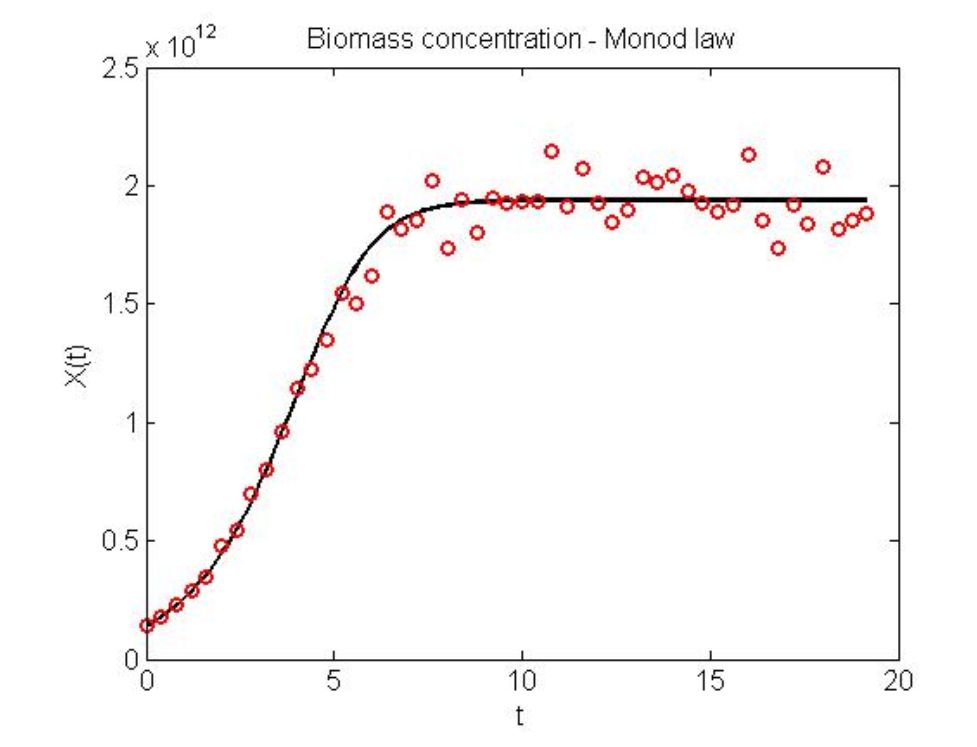
This course introduces various topics in dynamic system modeling, machine learning, parameter identification, and state estimation, with applications to biological and biomedical systems:

  • Introduction to population models and epidemics;
  • Dynamic models of bioprocesses (with examples in biopharmaceuticals, food, biofuels and environment);
  • Numerical simulation of dynamic systems;
  • Parameter identification (linear and nonlinear least-squares problems);
  • Neural networks in dynamic modeling (NN and Physics-NN models).
  • State estimation (observability of nonlinear systems and asymptotic observers);

Optimal Control and Estimation

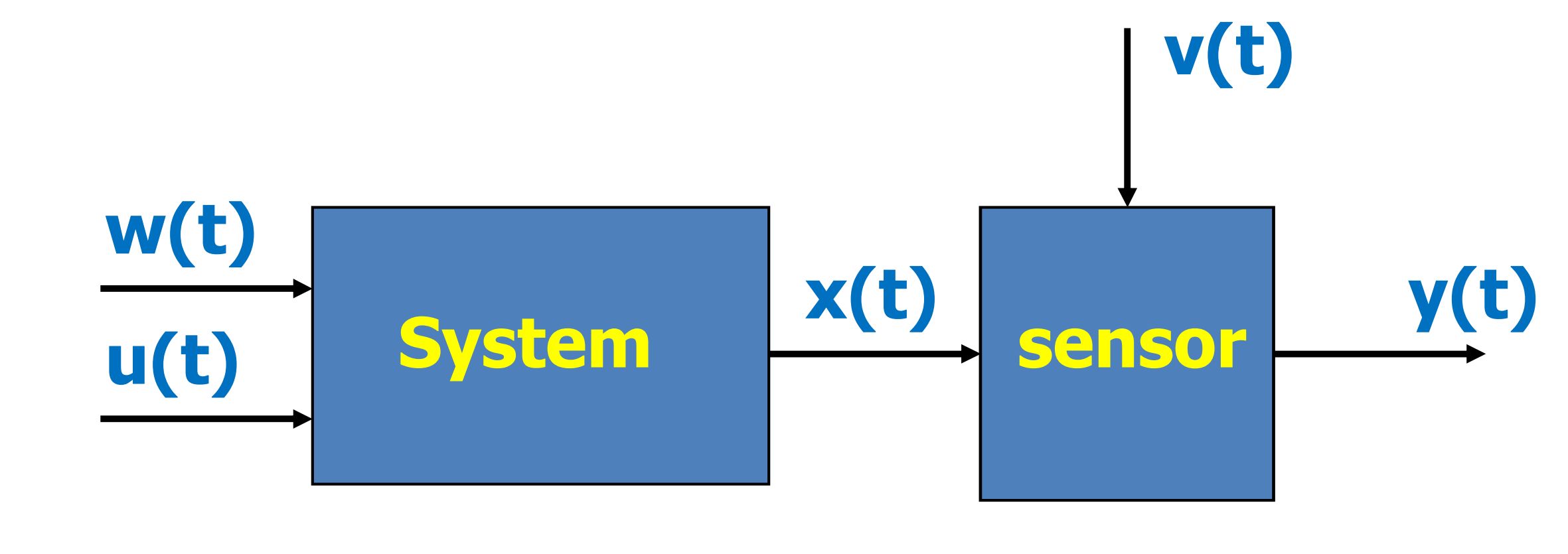
This course introduces optimal control and optimal state estimation of dynamic systems:

  • Linear quadratic regulator (discrete-time and continuous-time versions);
  • Pontryagin maximum principle;
  • Model predictive control;
  • Dynamic stochastic systems;
  • Kalman filtering.

Signaux et systèmes

  • Signaux et convolution de signaux - Transformées de Laplace et de Fourier et interprétation physique.
  • Introduction à la notion de système. Analyse temporelle et harmonique des systèmes linéaires permanents.
  • Approche des systèmes en boucle fermée : stabilité, précision et performances transitoires.
  • Principes généraux de dimensionnement d'un contrôleur.

Signaux, systèmes et commande

Signaux et convolution de signaux - Transformées de Laplace et de Fourier et interprétation physique. Introduction à la notion de système. Analyse temporelle et harmonique des systèmes linéaires permanents. Approche des systèmes en boucle fermée : stabilité, précision et performances transitoires. Principes généraux de dimensionnement d'un contrôleur.

State Observers and Estimators

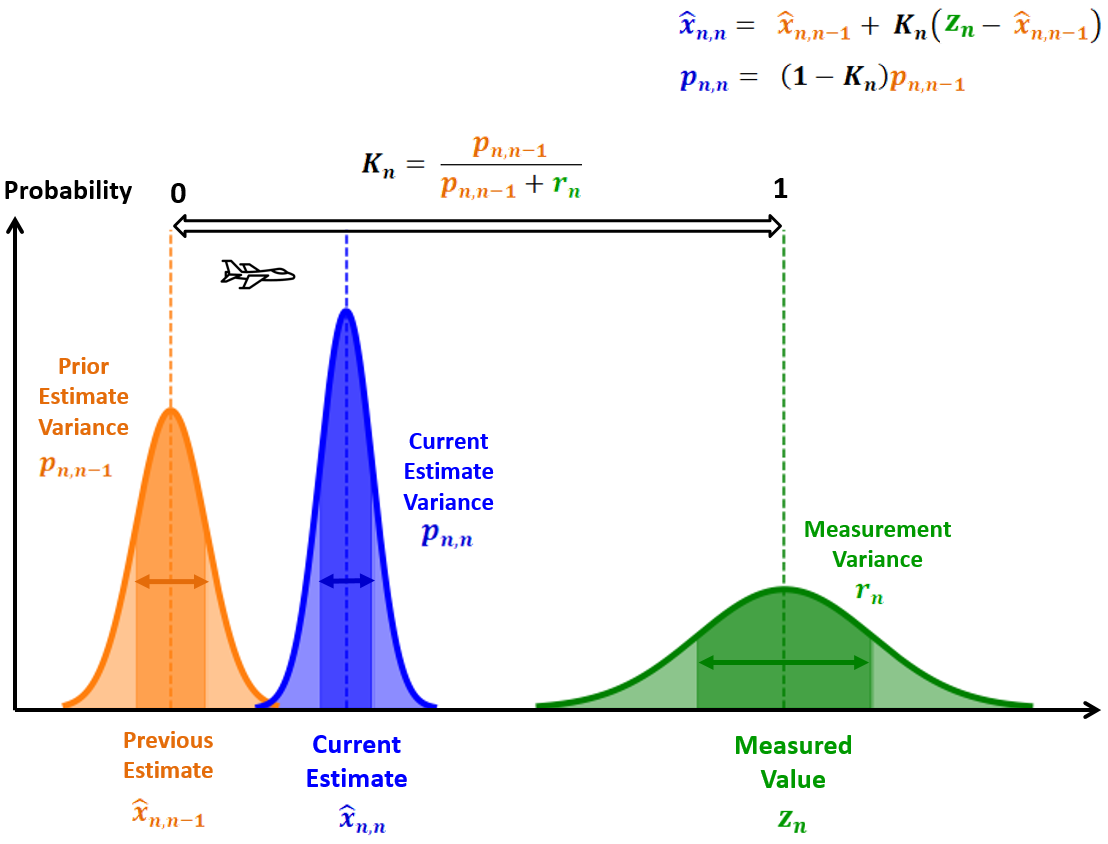
Kalman Filter in one dimension

This course addresses various aspects of stochastic state space representation of dynamic systems, Kalman filtering, together with a few examples and exercises.